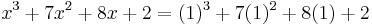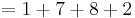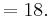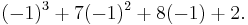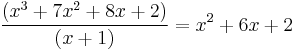Factor theorem

In algebra, the factor theorem is a theorem linking factors and zeros of a polynomial. It is a special case of the polynomial remainder theorem.

The factor theorem states that a polynomial $f(x)$ has a factor $(x - k)$ if and only if $f(k)=0$ .

Factorization of polynomials

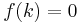Main article: Factorization of polynomials

Two problems where the factor theorem is commonly applied are those of factoring a polynomial and finding the roots of a polynomial equation; it is a direct consequence of the theorem that these problems are essentially equivalent.

The factor theorem is also used to remove known zeros from a polynomial while leaving all unknown zeros intact, thus producing a lower degree polynomial whose zeros may be easier to find. Abstractly, the method is as follows:

"Guess" a zero $a$ of the polynomial $f$ . (In general, this can be very hard, but math textbook problems that involve solving a polynomial equation are often designed so that some roots are easy to discover.)
Use the factor theorem to conclude that $(x-a)$ is a factor of $f(x)$ .
Compute the polynomial 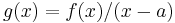$g(x) = f(x) \big/ (x-a)$ , for example using polynomial long division.
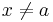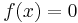Conclude that any root $x \neq a$ of $f(x)=0$ is a root of 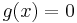$g(x)=0$ . Since the polynomial degree of $g$ is one less than that of $f$ , it is "simpler" to find the remaining zeros by studying $g$ .

Example

You wish to find the factors at

$x^3 %2B 7x^2 %2B 8x %2B 2.$

To do this you would use trial and error to find the first x value that causes the expression to equal zero. To find out if 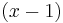$(x - 1)$ is a factor, substitute 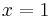$x = 1$ into the polynomial above:

$x^3 %2B 7x^2 %2B 8x %2B 2 = (1)^3 %2B 7(1)^2 %2B 8(1) %2B 2$

$= 1 %2B 7 %2B 8 %2B 2$

$= 18.$

As this is equal to 18 and not 0 this means 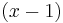$(x - 1)$ is not a factor of 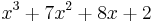$x^3 %2B 7x^2 %2B 8x %2B 2$ . So, we next try 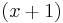$(x %2B 1)$ (substituting 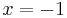$x = -1$ into the polynomial):

$(-1)^3 %2B 7(-1)^2 %2B 8(-1) %2B 2.$

This is equal to 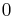$0$ . Therefore 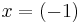$x=(-1)$ , which is to say 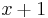$x%2B1$ , is a factor, and 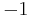$-1$ is a root of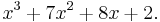 $x^3 %2B 7x^2 %2B 8x %2B 2.$

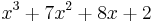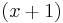The next two roots can be found by algebraically dividing $x^3 %2B 7x^2 %2B 8x %2B 2$ by $(x%2B1)$ to get a quadratic, which can be solved directly, by the factor theorem or by the quadratic equation.

${(x^3 %2B 7x^2 %2B 8x %2B 2) \over (x %2B 1)} = x^2 %2B 6x %2B 2$

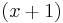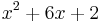and therefore $(x%2B1)$ and $x^2 %2B 6x %2B 2$ are the factors of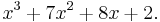 $x^3 %2B 7x^2 %2B 8x %2B 2.$

Formal version

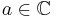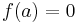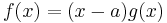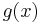Let $f$ be a polynomial with complex coefficients, and $a$ be in an integral domain (e.g. $a \in \mathbb{C}$ ). Then $f(a) = 0$ if and only if $f(x)$ can be written in the form $f(x)=(x-a)g(x)$ where $g(x)$ is also a polynomial. $g$ is determined uniquely.

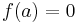This indicates that those $a$ for which $f(a) = 0$ are precisely the roots of $f(x)$ . Repeated roots can be found by application of the theorem to the quotient $g$ , which may be found by polynomial long division.